Reverse Time Migration (RTM) Technology
Reverse Time Migration (RTM) has become the method of choice for seismic imaging in complicated areas. The method is based on directly solving the wave equation in the time domain (as opposed to the frequency domain). RTM can accurately handle any variation in subsurface material properties, and has no limit in imaging steep dips. RTM is not based on ray tracing and hence can perform in situations where Kirchhoff ray based migration breaks down.
Historical Developments
The use of computer based migration started in the early 70s. Due to limitations in computer power, various methods were developed to apply depth migration while keeping the computational cost low. These included the use of simpler versions of the wave equation (Claerbout and Doherty, 1972), the use of ray trace based migration (Schneider 1978), the use of direct mapping from time to depth (Stolt, 1978) and the use of the downward extrapolation (Gazdag, 1978). Having limitations in each of the above methods, a method based on reverse modeling was introduced at 1983 in three separate publications. George McMechan published in Geophysical Prospecting, the paper “Migration by extrapolation of time dependent boundary values”, Dan Whitmore published in the SEG extended abstracts, the paper “Iterative Depth Migration by Backward Time Propagation", and the paper that coined the term RTM was published in Geophysics by Dan Kosloff and Edip Baysal “Reverse time migration." All of the above publications applied to 2D stack data where the migration was applied as a post stack migration.
Although the publications of RTM demonstrated the benefits of the algorithm, it was not adopted by the industry as a common algorithm for application of depth migration. The reasons were explained by Irshad Mufti (Irshad Mufti, Jorge Pita and Ross Huntley, 1994, “Finite-difference depth migration of exploration-scale 3-D seismic data”), by (a) the creation of reflected wave fronts during the extrapolation step, and (b) the need to use a much smaller grid in order to avoid numerical dispersion. In this publication however, Irshad Mufti set the link between the use of highly parallel computers to the ability to use RTM in a production processing environment. These theoretical limitations, together with the limitations in computer power, resulted in the use of RTM mostly in university settings, as was shown in 1996 by Jinming Zhu and Larry Lines in the SEG abstract “Comparison of Kirchhoff and reverse‐time migration methods with applications to prestack depth imaging of complex structures."
In the past decade, computer hardware power increased so dramatically that application of 3D prestack RTM in industrial settings became possible. Moreover, the ability of the industry to construct complex velocity (and anisotropic) models removed the imbalance between the quality of the velocity models and the ability of PSDM algorithms to handle such models. This allowed RTM PSDM to become the algorithm of choice when imaging any geological setting that requires a complex velocity (or anisotropic) model. Today, three decades after the introduction of RTM PSDM, the algorithm is widely used by academia, the industry and in many exploration and development projects that involve imaging subsalt structures in deep water environment.
Technical Background
RTM principal is based on reversing the forward modeling operation. In forward modeling, we input a velocity model, select the source location, and by numerically solving the wave equation in incremental time steps, wave propagation is computed in the subsurface. RTM operation consists of inputting the wave field recorded at the surface, and by stepping backwards in time, propagate the seismic events to the subsurface location where they were generated.
Post Stack Migration
In the case of post stack depth migration, instead of simulating wave propagation for a single shot location, we insert a source function at every velocity boundary location. This is known as the ‘exploding reflector’ concept (Jon F. Claerbout, Imaging the Earth’s Interior, 1996). For forward modeling we start the wave propagation simulation at time=0 and carry the propagation until time=T. For migration we reverse the operation by starting the wave propagation at time=T and propagating backwards until time=0. By doing this, when time=0 is reached, the reflections initiated at the subsurface velocity boundaries and recorded at the surface will reach back to their exact subsurface locations. This operation is called ‘post stack reverse time migration."
Prestack Migration



In the case of prestack modeling, wave propagation starts at the surface, propagates downwards, reflects at the velocity boundaries and is recorded back at the surface. In order to ‘map’ the surface recorded wave fronts back to the subsurface locations from where they were reflected, we need to back propagate the recorded wavefronts from the surface back to the subsurface. Since we don’t know at what location and depth each wavefront was reflected from, we use the fact that at a reflection point the incident wave and the reflected wave are time coincident. Based on this assumption, we perform the three step operation: (1) Simulate the wavefront propagating from the source location; (2) Downward propagate the recorded wavefronts from the surface to the subsurface; (3) At every time step cross-correlate the simulated wavefield with the downward propagated wavefield. At every subsurface location that the simulated wavefield correlates with the downward propagated recorded wavefield, an image will be constructed. The above 3-step procedure is the basis for prestack Reverse Time Migration.
The above figures 1-3 demonstrate the wave field propagation from the source. Figures 1-3 below show the downward propagation of the receiver wavefield. Figures 1-6 below show the result of the cross correlation between the source wavefield and the receiver wavefield.



In order to successfully accomplish the above procedure, several key numerical operations need to be defined. Numerical solution of the wave equation calls for two mathematical operations: (a) Computation of numerical derivatives and (b) Computation of time integration. In order to ensure numerical stability of the solution scheme, an appropriate time step needs to be selected, and in order to ensure wave propagation with minimal numerical dispersion, the appropriate frequency band needs to be defined. In most cases, finite differences operators are used as the mechanism for time integration. To ensure numerical stability of the solution scheme, the time step for wave propagation needs to be very small, resulting with accurate time integration when second order finite differences operators are used. However, in order to be able to accomplish accurate wave propagation with minimal or no numerical dispersion, a careful selection of the derivative operators need to be done.






Challenges and Solutions
The computational cost of RTM PSDM is very high. In order to be able to migrate a broader frequency range, a small size cell needs to be used as the numerical grid. This results with large computer memory requirement as well as an enormous number of floating point operations.
These two limitations lead very often to the use of a band limited selection of the input data, resulting with low frequency RTM PSDM. The motivation to overcome these limitations in implementing of RTM PSDM leads us to develop solutions both in software and in hardware.
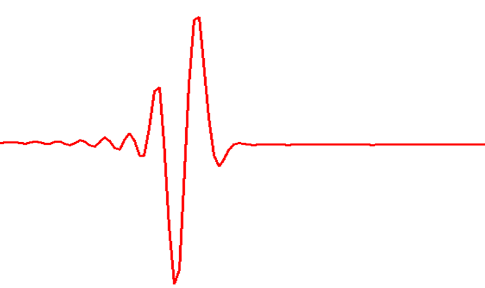

The first goal is to be able to migrate the full frequency range without creating significant numerical dispersion of the propagated wavefield. A solution to that was accomplished by using newly developed recursive operators that are able to accurately compute spatial derivatives without the need to use a very small operational grid (Acoustic and elastic numerical wave simulations by recursive spatial derivative operators, Kosloff et al. 2010). Figure 1 above shows a source wavelet after wave propagation using an 8th order finite difference operator. Computed on the same numerical grid and input frequency, Figure 2 shows the same source wavelet after wave propagation using recursive operators. The source wavelet computed using recursive operators does not include any numerical dispersion. This enables us to use a boarder spectrum source wavelet as well as higher frequency range of the input data, resulting with higher frequency RTM PSDM.


Figures 3 and 4 above show a simulated time section produced using 8th order finite difference and recursive operators, both calculated using the same numerical grid and the same frequency range. Figures 5 and 6 below show the corresponding RTM PSDM. Both simulated time sections and RTM depth migrated sections produced using recursive operators show minimal amount of numerical dispersion compared to the finite difference operators.
Computer Implementation
The second goal in the implementation of RTM PSDM is to adapt the software to a specific hardware configuration capable of performing very high number of floating point operations in a short time. SeismicCity was one of the first companies to pioneer the use of NVIDIA GPUs for use in application of RTM PSDM.
In the past several years we have improved our RTM technology to use hybrid GPU/CPU computer hardware, where both compute components can take part in the computation of wave propagation and wave-field cross correlation. The current SeismicCity GPU/CPU RTM PSDM implementation is based on computation of spatial derivatives using recursive operators (GPU implementation of minimal dispersion recursive operators for reverse time migration, Bartana et. al. 2015). This results with RTM PSDM implementation that can be economic and provide the data quality expected from the algorithm.


Industrial Use
RTM PSDM has now been used by the industry for several years. The algorithm has proven to produce reliable images in various geological settings. However, the development of RTM PSDM has still not been completed. Improvements to the RTM algorithms will include the ability to migrate the full frequency range, the use of more complex anisotropic models and reduction of algorithm generated numerical arttifacts. Additionally, RTM PSDM is now used as the compute engine for a velocity estimation procedure called full waveform inversion. As computer hardware continues to improve, we expect RTM PSDM use to expand to new geological settings and to produce PSDM data where amplitude preservation is needed.





